Основы Пролога. Часть 2

Fundamental Prolog
Часть 1 Часть 2

In this tutorial you will learn about some more fundamental ideas of Prolog programming; continuing from where we left off in the Part 1 of this tutorial (Fundamental Prolog). In this tutorial, we are going to concentrate on how data is modeled in Prolog, before we can perform actions on them. Hence, there are not much examples concerning code execution here. We are assuming that you are already familiar with the issues concerning execution strategy and how side effects convert the logic of a Prolog program into the desired results.

As in the Part 1 of this tutorial, we shall continue to use the PIE environment to develop and learn Prolog. We shall get into the Visual Prolog IDE only in the latter parts of this series.

Functors

In Part 1 of the tutorial, all the people were represented as "Bill", "John" and "Pam" etc. Now "Bill", "John" and "Pam" are just the names of the individuals. The values of the names are simple data types or simple domains. In the case of the names of the people, the simple domain was a string. Other simple domains would be numbers (e.g.: 123 or 3.14), symbols (e.g.: xyz or chil_10), and characters (e.g.: '5' or 'c').

However, individuals are represented by more characteristics than just their names. What if we need to represent all those characteristics together, instead of representing just their names? That means, we need some mechanism to represent compound domains; a collection of simpler domains held together.

In the first part of this tutorial, we had tried putting together several characteristics of individuals together, (like the name and the gender), by inserting facts into the PIE system that concentrated on entities instead of relationships. Thus we had given the following facts to the system:

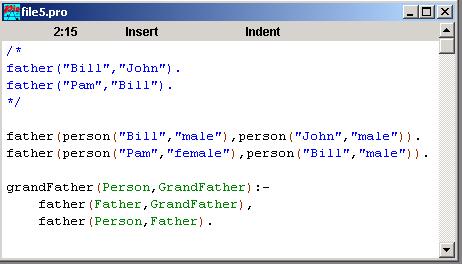
person("Bill", "male").
person("John", "male").
person("Pam", "female").

However, there is another elegant method to sharpen our focus on the entities being represented.

We can package both the Name and the Gender into a package using a formalization known as a compound domain. The entire package can then be represented using a logical variable inside any Prolog clause, just like any other variables. For example, the above facts can be generically represented in a compound domain thus:

person(Name, Gender)

Note that the above statement is neither a fact nor a predicate. Logically, it states that there is some compound domain called person in the system, each of which has two characteristics, represented by the logical variables Name and Gender. The word person is known as a functor, and the variables are its arguments. We shall now package our facts using these functors.

As a compound domain always has a functor, we shall henceforth use the term functor in this tutorial, to represent the respective compound domain.

For now, let us modify the first example of the previous tutorial, so that we use our newly defined functor person.

Please note that in the PIE (Prolog Inference Engine) that we are using, we can directly use a compound domain without any prior intimation to the Prolog engine (for example. we need NOT define a predicate or a fact called person for our code to work).

If you study the two facts for the father relationship, you would notice that the persons described are richer than what was done before (The earlier code is commented out in-between the tokens /* and */ .). This time, each person is described with both the person's name and his/her gender, using the person functor, whereas in the earlier tutorial (Fundamental Prolog (Part1)) we were only using the person's name.

After you have written the new code, ensure that the PIE engine is reset. Use Engine -> Reset. Then, you re-consult the code using Engine -> Reconsult.

As before, on a blank line in the Dialog window type a goal (without the "?" sign- in front).

For example:

When the caret is placed at the end of the line, press the Enter key on your keyboard. PIE will now consider the text from the beginning of the line to the caret as a goal to execute. You should see the following result:

Now, you will notice that the results that are yielded are richer than what you got previously (See Tutorial 04: Fundamental Prolog (Part 1)).

Refining Further

If you take a look at the grandfather predicate, you would notice that it has a subtle bug: A person would have two grandfathers: one from the mother's side and one from the father's side, but the grandfather predicate as defined earlier would only yield the grandfather on the father's side.

Hence the grandfather predicate should be re-written as follows:

grandFather(Person, TheGrandFather):-
     parent(Person, ParentOfPerson), 
     father(ParentOfPerson, TheGrandFather).

In this predicate the logic states that a father of any parent could be the grandfather of the person in consideration.

For that predicate to work, we need to define a predicate called father using the person functor. This predicate would troll through a database of facts explaining the "parents" defined in the system. This is a more elegant method for finding out the fathers, instead of presenting them as facts (as shown previously) because later on we can extend this concept to find out "mothers" in a similar fashion.

This can be done in either of the following ways:

/*1st version */
father(P, F) :-
    parent(P, F), 
    F = person(_, "male").    %Line 2

or

/* 2nd version */
father(P, person(Name, "male")) :-
    parent(P, person(Name, "male")).

The logic behind both the versions is the same, but the manner in which the logic is indicated to the Prolog engine is different. In the first version, the code in Prolog systematically examines each parent fact asserted into the code, and sees if the first logical variable (P) matches that passed down from the predicate head. If the variable does match, it checks if the second argument consists of a person functor, whose second argument is the string literal "male".

This example shows one important feature of functors: The arguments of a functor can be taken apart and examined using regular Prolog variables and bound values (like the string literal in this example) If you see Line 2 (Look at the side of the comment %Line 2 in the code for the first version), you would notice that we have used an anonymous variable (the underscore) for the first argument of the person functor as we are (in that predicate) not interested in the name of the father.

The second version also does the same thing as the first one. But this time, as the set of parent facts is examined; on arriving at the correct value for P, the code halts and returns the correct functor data back to the predicate head, provided the second argument of that functor is the string literal "male". If you note, the functor was NOT bound to any intermediate Prolog variable, as it was done in the first version.

The second version is much terser than the first one, and sometimes this method of writing the code can be less legible to beginners.

Let us now use this code in a complete example, where we will give a suitable set of person' facts:

Now, after you re-consult the above code into PIE, and give the following goal:

grandFather(person'("Pam", "female"), W)

the results would be as follows:

Functors and Predicates

Technically, a functor represents a logical function that binds several domains together. In simpler words, a functor is a mechanism that teaches the Prolog Engine how to put together data from its component parts. It effectively puts parts of the data into a common box. You can also retrieve the parts subsequently, whenever required (like seen the previous examples). It may look like a Prolog fact or a predicate call, but it is not. It's just a piece of data, which you can handle in much the same way as a string or a number.

Please note that a functor has nothing to do with a function in other programming languages. It does not stand for some computation to be performed. It simply identifies the compound domain and holds its arguments together.

When you study the above example, you would notice that nothing special need to be done when logical variables are used to stand in for data represented by functors. The logical variable that is used to stand in for such data, is written just like any other logical variable: A word starting with a capital letter. Thus, if we take a look at the grandFather predicate in the example in this tutorial; you would notice that nothing has changed when you compare it with the same predicate that was defined in the earlier tutorial (Fundamental Prolog (part 1)). After all, the logic of that predicate has not changed. So, you would not find any changes to the variables used inside that predicate.

The biggest advantage of using a functor is that you are free to change the internal arguments of the functor without changing much of the predicates that uses such a functor as you keep revising the code.

That means, if you decide (in a later version of the code you are writing) to have one more argument for the person, you still need not change anything in the grandfather predicate.

Functors as Arguments

In the previous section, the person functor was having two arguments: the Name and the Gender. Both happened to be simple domains i.e. constants such as "Bill" and, "male". However, there is nothing that prevents us from putting a functor itself as an argument of another functor.

Suppose, you wanted to define a functor for a couple (i.e. a husband and a wife). This is an example of how you would use such a functor:

myPredicate(ACouple):-
    ACouple = couple(person(Husband, "male"), person(Wife, "female")), 
    ...

In this example, you would notice that the functor is defined by two functors, each of which is a mixture of variables and constants. This can be done to reflect the logic of the data being represented. The logic used here is that a husband is always a "male" and wife is always a "female"; and a couple consists of a husband and a wife. All of which is consistent with the most common interpretation of what one means by a couple.

Though in PIE you cannot predefine the kind of grammar functors can actually have; in Visual Prolog you can make such definitions. The advantage of defining a functor in such a manner is that later, when you create actual data using this functor, the Prolog engine will always check if the data being created was consistent with the grammar that data was supposed to adhere to.

This comes to another characteristic of functors: the couple functor has been defined with two arguments and the position of these arguments reflects their logical association. It was explained in the first part of this tutorial, that the positions of the arguments of predicates have to be formalized by the programmer, who designs the code. Once formalized; the same positional formalization should be consistently used.

The same strategy applies to the creation of functors too: In the case of the couple functor, it so happened that we decided to represent the husband as the first argument, and the wife as the second one. Once this is done, then whenever data is created using such a functor, then we need to ensure that the husband is always at the first position, and the wife in the second (in spite of what the women's lib people may say!)

Now, when we look back on the couple functor, someone can correctly argue that if were so sure that the first argument is always a husband (who is always a male), and the second one is always a wife (who is always a female) then what is the need for making the arguments of the couple functor also as functors? Hence, an example with a more simplified couple functor would be as follows:

myPredicate(ACouple):-
    ACouple=couple(Husband, Wife), 
    ...

Hence; let us revert back to using functors for the husband and wife... but this time we will use them, because we are not sure which position is for the husband and which is for the wife.

myPredicate(Couple):-
     Couple = couple(person(PersonsName, PersonsGender), person(SpouseName, SpouseGender)), 
     ...

In the above functor, both the following examples make logical sense:

myPredicate(C1):-
    C1=couple(person("Bill", "male"), person("Pam", "female")), 
    ...
 
/* or */
myPredicate(C2):-
    C2=couple(person("Pam", "female"), person("Bill", "male")), 
    ...

It should be pointed out that in the PIE (and many other Prolog Engines), there is no way to indicate whether a functor will receive simple domain or compound domain arguments, by looking at the variables that define the functor. This stems from the fact that in PIE, compound domains are directly used, without being declared anywhere, other than in the mind of the programmer.

For example, if you wanted to use a compound domain as:

person(Name, Gender)

then PIE would as easily accept a logical variable such as:

regardingAPerson(Somebody):-
    Somebody = 
        person("Pam", 
            person("Pam", 
                person("Pam", 
                   person("Pam", "female")
                )
            )
        ), 
    ...

which actually does not make any logical sense, in the current context. Luckily, Visual Prolog, does a much better job of differentiating between simple domains and compound domains, so, when you get to the latter tutorials, you would not have any such problems.

Recursion Using Functors

When data is described using functors, it can be treated like any other piece of data. For example, you can write a predicate that can be made to recursively search through data which used compound domains using functors.

Let us get back briefly to the ancestor predicate, which we had used in the first part of the tutorial.

In order to determine if somebody is an ancestor of someone else, we used a recursive definition for the predicate, i.e. a definition that is defined in terms of itself. like this:

ancestor(Person, Ancestor) :- parent(Person, Ancestor).
ancestor(Person, Ancestor) :- parent(Person, P1), ancestor(P1, Ancestor).

This declaration states that a parent is an ancestor, and that an ancestor to a parent is also an ancestor. If you examine the variables in the above definition, it can very well stand for either simple domains or compound domains.

Let us define the data thus:

parent(person("Bill", "male"), person("John", "male")).
parent(person("pam", "female"), person("Bill", "male")).

If we now ask PIE to solve the following goal,

P=person("pam", "female"), ancestor(P, Who)

...this is what we will get:

The PIE engine has recursively examined the parent facts to reveal the two possible solutions to the answer. By the way, in the above query, you would also notice that we have bound a variable P to the person compound domain when specifying the goal to PIE. This was done to make the code more readable but it also demonstrates the fact that we can bind a piece of data specified as a compound domain into any Prolog variable.

Strategies for Using Functors

Software will be only as good as allowed by the modeled data. By the term modeling, we mean the establishment of a relationship between the subset of the outside real-world that is being tackled with the internal data structures of the software. If the modeling of data is poor, then it is likely that the software will also be poor; or at best, inefficient. This is true of any software written in any programming language. That was the reason in the latter part of the earlier tutorial (Fundamental Prolog (part 1)), we had tried to focus on the entities and tried to correct the situation by inserting richer facts. Similarly, we introduced the concept of functors in this tutorial to get even more clarity on the data regarding entities that are being modeled.

The advantage of Prolog is that it allows easy description of the real-world data in a form that can be internally utilized by the code in an efficient manner. Simultaneously, it also makes the code very readable by fellow programmers who are working together on a project.

Functors can be used to create any type of compound domain to help in this modeling process. You would have to carefully examine the various parts of real-world data that you plan to process and convert them using functors (and other data types that you would encounter in future tutorials) keeping in mind their usage in all critical parts of the software. Some data structures that were useful in one area of the software may prove to be a hindrance in other areas.

You should take a holistic approach while zeroing in on the functors (and other data structures) you plan to use in your software. Pause and look around at all the corners of your software. Only then should you code the necessary functors.

Just thinking carefully about the data structures is not the only thing that is required. You would also need to (often simultaneously) write/modify the various goals and sub-goals (i.e. predicates) and then use the data developed thus far in those predicates. The side effects of attaining those goals and sub-goals would make your software work and you can get valuable feedback with which you can further refine your data structures.

In this tutorial, we have not fleshed out a software design holistically. We have only nibbled at bits and pieces of data which establishes the feel for some kind of real-world data concerning relationship between people (parents, grandparents, families, ancestors etc.) In forthcoming tutorials, we will use this experience to establish a red thread that connects all these tutorials together; eventually ending up with a useful software that requires such data structures.

Conclusion

In this lesson we learnt that data can comprise of simple domains, or they can be compound domains represented using functors. We found that the arguments of functors must be positionally consistent with the logic they were meant to represent. We understood that a functor need not have just simple domains as arguments, but it can also have other functors as arguments. We then learnt that data represented as functors can be used like any regular Prolog variable, and we can even perform all operations; including recursion, on such data.

We also learnt that we must spend time modeling our subset of the real world for which we are developing the software, and get a feel for the data. We should simultaneously experiment with the predicates that you may wish to use with the data that is being modeled, so that they can be refined further.